Standard Friction Equation

The standard friction equation is the relationship between the resistive force of sliding friction for hard surfaces, the normal force pushing the two surfaces together and the coefficient of friction number for the two surfaces. When applied to sliding friction of hard surfaces, the equation implies that friction is independent of the area of the surfaces in contact. This equation can also apply to soft surfaces, rolling friction and fluid friction, but the coefficient of friction may depend on area, shape and viscosity factors.

Questions you may have include:

• What is the standard friction equation?

• What is the normal force?

• What is the coefficient of friction?

Standard friction equation

The standard equation for determining the resistive force of friction when trying to slide two solid objects together states that the force of friction equals the coefficient friction times the normal force pushing the two objects together. This equation is written as:

Fr = μ*N

where

Fr is the resistive force of friction,

μ is the coefficient of friction for the two surfaces (Greek letter "mu"), and

N is the normal or perpendicular force pushing the two objects together.

Fr and N are measured in units of force, which are pounds or newtons. μ is a number between 0 (zero) and ∞ (infinity).

Applies to static and kinetic

This equation applies to both static and kinetic sliding friction. Static friction is the friction before an object starts to slide. Kinetic friction is the friction when the object is actually moving or sliding.

Static friction and kinetic friction have different coefficient of friction values.

Independent of area for sliding hard surfaces

An interesting result of this equation is that in the case of sliding friction of hard surfaces, the friction is independent of the area of the surfaces. In other words, it is just as difficult to move a 1 square-cm object as a 1 square-meter object, if they both are pressed to the surface with the same amount of force.

This is not intuitive. You would think that there is more friction when the surfaces are larger, but the friction equation states otherwise. You can verify this fact with experiments.

Soft, adhesion, rolling and fluid

In situations where the surfaces deform or there is molecular adhesion, the friction is not independent of the areas in contact. In these cases surface area usually comes into play. This is also true for rolling and fluid friction.

When solid surfaces are soft and deform or when one material is a fluid, the shape of the solid object may be a factor.

Although the standard friction equation still holds, the coefficient of friction may have area, shape and other factors included in it.

Normal force

The normal force is the force pushing the two objects together, perpendicular to their surfaces.

Sanding block example

For example, if you push a sanding block against a wooden desk you were sanding, the normal force would be the amount of force you pushed on the block. You would move the sanding block in one direction and the force of friction would be in the opposite direction.

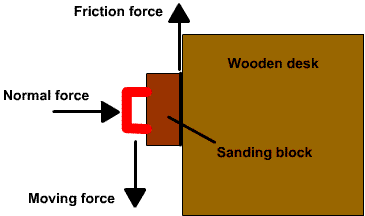
Applying normal force on sanding block and wooden desk

Two normal forces

Sometimes, two normal forces are used to cause the friction.

One example is a pair of pliers that applies a normal force on both sides of a piece of wood that the pair of pliers is holding. Another example are the calipers on automobile disc brakes that apply a force on both sides of the metal disc to slow down the car.

Weight as normal force

The normal force N can be caused by gravity instead of some applied pressure. This would be in situations where you slide a heavy object across the floor or some horizontal surface. Since weight is the force pushing the objects together, the friction equation becomes:

Fr = μ*W

where W is the weight of the object.

Thus if a box weighs 100 pounds and the coefficient of friction between it and the ground is 0.7, then the force required to push the box along the floor is 70 pounds.

Likewise if a box weighs 500 newtons is placed on ice with a coefficient of friction of only 0.001, then it would only take 0.5 newtons to move the box.

Weight on incline

If the weight is on an incline, the normal force will be reduced by the cosine of the incline angle.

N = W*cos(a)

where:

N is the normal force on the incline,

W is the weight,

a is the incline angle, and

cos(a) is the cosine of a.

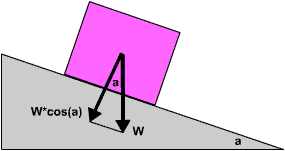
Normal force is weight times cosine of angle

Coefficient of friction

The coefficient of friction, μ (mu), is a number related to the two specific surfaces that are in contact with each other. It is very dependent on the roughness of each surface and how the materials slide against each other.

Established by experiment

Although there are charts listing average values of the coefficient of friction for various materials, the only true way to establish the number is by experiment and testing or empirical measurements. Also, there are no good formulae or equations to predict μ.

By dividing both sides of the standard friction equation Fr = μ*N by N, you will get the equation:

μ = Fr/N

This relationship indicates that if you can measure the friction force Fr and know the normal force N pushing the two objects together, you can determine the coefficient of friction μ.

Wide range of numbers

The coefficient of friction can range between 0 (zero) and ∞ (infinity).

Close to zero

When μ = 0, there is no friction. If μ is close to 0, there is little friction. For example, leather-soled shoes on slippery ice has a very small coefficient of friction, close to zero. That is why you can easily slide on ice or even take a fall. Even rubber-soled shoes on ice has a very small coefficient of friction.

Close to infinity

Many students and teachers mistakenly think that μ must be less than 1. That is incorrect, since Fr could be many times the normal force.

One extreme example is if you glued an object to another. The resistance to moving the objects would be very large and the coefficient of friction would also be very large. If the glue was so strong that they could never be slid against each other, then μ would equal infinity.

The reason people think that μ must be less than 1 is probably since most listing of coefficients of friction have values less than 1. That is because most materials of interest usually slide relatively easy on each other.

Examples of coefficient

The following table shows the coefficient of sliding friction for a number of materials. Note that the static coefficient is larger than the kinetic coefficient.

Coefficient when surfaces not hard and sliding

In the case where a surface is soft, there is molecular adhesion, and in rolling and fluid friction, the coefficient of friction is not a simple number. The coefficient may be dependent on the area of the surfaces, the amount of deformation, the amount of adhesion, the shape of the surfaces, the radius of the wheel or the viscosity of the fluid.

What this means is that although the standard friction equation holds in these cases, the coefficient of friction will only hold for a specific configuration. In other words, you can't accurately give something like the coefficient of rolling friction for a rubber tire on pavement without stating the type of rubber, area on the pavement, inflation of the tire, and its tread pattern.

In conclusion

The standard friction equation is the relationship between the resistive force of sliding friction for hard surfaces, the normal force and the coefficient of friction for the two surfaces. When applied to sliding friction of hard surfaces, the equation implies that friction is independent of the area of the surfaces in contact. This equation can also apply to soft surfaces, rolling friction and fluid friction, but the coefficient of friction may depend on other factors.