|
When visible light enters a transparent
material such as glass at an angle, the direction of the
light is refracted or bent at a different angle. The
angle is determined by the initial angle and the index
of refraction of the two materials. Snell's Law is an
equation that determines the angle at which a ray or
beam of light is refracted. When the light passes from a
material of high index of refraction to low index of
refraction, there is an angle at which the light starts
to be reflected at the interface of the materials. This
is called the critical angle for refraction.
Questions you may have include:
Snell's Law
Snell's Law determine the angle at which
a beam of light bends, according to the initial angle
and the index of refraction of the two materials.
If A is the index of refraction of the
first material for and a is the angle of the incoming
ray or beam of light with respect to the perpendicular
or normal to the surface, then b will be the angle to
the normal of the ray in the second material where B is
its the index of refraction.
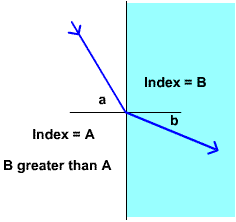
Light is bent going from first material
to second
The Index of Refection in material B
equals the speed of light in a vacuum (c) divided by the
speed of light in the material (cB).
B = c / cB
Since index B is greater than index
A,
the speed of light in material B is less than the speed
in material A. Thus, according to Snell's Law, the angle
b is less than the angle a.
Snell's Law is written as:
A*sin(a) = B*sin(b)
where sin(a) is the sine of angle
a and sin(b) is the sine of angle b.
Calculating values
Typically, you want to find angle b or
how much the light will be bend in the second material.
Using some Algebra, Snell's Law can be rewritten as:
sin(b) = A*sin(a)/B
or
b = arcsin[A*sin(a)/B]
where arcsin[A*sin(a)/B] is the arcsine
or angle whose sine is A*sin(a)/B.
Thus if the first material is air (index
approximately = 1), the incoming angle is 30o and the
second material is glass with an index = 1.5, you can
calculate the angle of the light in glass.
sin(b) = A*sin(a)/B
sin(b) = 1*sin(30o)/ 1.5
sin(b) = 0.5/ 1.5 = 0.33
b = arcsin(0.33) = 19.5o
Thus, if light hits glass at 30o, its
angle will change to 19.5o within the glass. Of course,
if it is a glass plate, you will then use the opposite
to obtain the exit angle of 30o back into air.
Critical angle for refraction
An interesting thing happens when light
is going from a material with higher index of refraction
to a lower index, such as going from water to air. There
is an angle at which the light will not pass into the
other material and will start to be reflected at the
surface. This is call the critical angle of refraction.
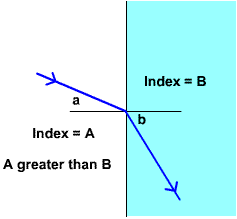
Light going from high index to low
In the figure above, you can see that
angle b is larger than angle a when index
A is larger
than index B. At some angle a, angle b will equal 90
degrees.
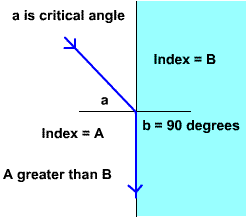
Light at critical angle for refraction
Using Snell's Law, we can calculate this
critical angle. Let the first material be water with
index of refraction = 1.33, and let the second material
be air with index = 1.
We want to find angle a:
sin(a) = B*sin(b)/A
sin(a) = 1*sin(90o)/1.33
since sin(90o) = 1,
sin(a) = 1/1.33 = 0.75
a = arcsin(0.75) = 48.6o
This is the critical angle. When angle a
is greater than that angle, the light will be reflected.
At angles greater than the critical
angle for refraction, the light demonstrates an internal
reflection.
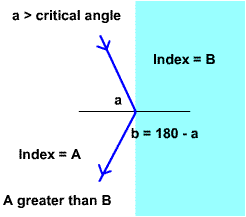
Internal reflection of light
When a is greater than the critical
angle for refraction, the light is reflected off the
interface of the two materials just like a mirror. (a >
means "a greater than".)
The Law of Reflection holds where the
incident angle equals the reflected angle. Thus b = 180o
- a.
You can see this effect by filling a
glass with water and observing it from below the water
line.
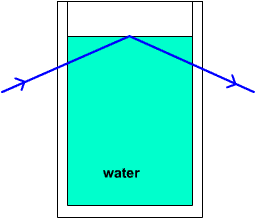
Internal reflection in glass of water (neglecting refraction from the glass)
Snell's Law states that when visible
light enters a transparent material at an angle, the
direction of the light is refracted or bent at a
different angle. Snell's Law is an equation that
determines the angle at which a ray or beam of light is
refracted. When the light passes from a material of high
index of refraction to low index of refraction, there is
an angle at which the light starts to be reflected at
the interface of the materials. This is called the
critical angle for refraction. |