Resonant filters
So far, the filter designs we've
concentrated on have employed either capacitors or
inductors, but never both at the same time. We should know
by now that combinations of L and C will tend to resonate,
and this property can be exploited in designing band-pass
and band-stop filter circuits.
Series LC circuits give minimum impedance at
resonance, while parallel LC ("tank") circuits give maximum
impedance at their resonant frequency. Knowing this, we have
two basic strategies for designing either band-pass or
band-stop filters.
For band-pass filters, the two basic
resonant strategies are this: series LC to pass a signal, or
parallel LC to short a signal. The two schemes will be
contrasted and simulated here:
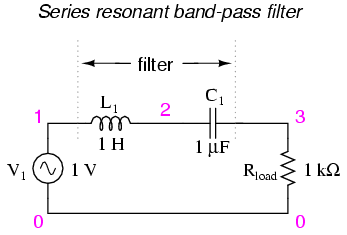
Series LC components pass signal at
resonance, and block signals of any other frequencies from
getting to the load.
series resonant bandpass filter
v1 1 0 ac 1 sin
l1 1 2 1
c1 2 3 1u
rload 3 0 1k
.ac lin 20 50 250
.plot ac v(3)
.end
freq v(3) 2.512E-01 3.981E-01 6.310E-01 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
5.000E+01 3.291E-01 . * . . .
6.053E+01 4.063E-01 . .* . .
7.105E+01 4.870E-01 . . * . .
8.158E+01 5.708E-01 . . * . .
9.211E+01 6.564E-01 . . .* .
1.026E+02 7.411E-01 . . . * .
1.132E+02 8.210E-01 . . . * .
1.237E+02 8.910E-01 . . . * .
1.342E+02 9.460E-01 . . . * .
1.447E+02 9.824E-01 . . . *.
1.553E+02 9.988E-01 . . . *
1.658E+02 9.967E-01 . . . *
1.763E+02 9.796E-01 . . . *.
1.868E+02 9.518E-01 . . . * .
1.974E+02 9.174E-01 . . . * .
2.079E+02 8.797E-01 . . . * .
2.184E+02 8.408E-01 . . . * .
2.289E+02 8.026E-01 . . . * .
2.395E+02 7.657E-01 . . . * .
2.500E+02 7.307E-01 . . . * .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Load voltage peaks at resonant frequency (159.15 Hz)
A couple of points to note: see how there is
virtually no signal attenuation within the "pass band" (the
range of frequencies near the load voltage peak), unlike the
band-pass filters made from capacitors or inductors alone.
Also, since this filter works on the principle of series LC
resonance, the resonant frequency of which is unaffected by
circuit resistance, the value of the load resistor will not
skew the peak frequency. However, different values for the
load resistor will change the "steepness" of the Bode
plot (the "selectivity" of the filter).
The other basic style of resonant band-pass
filters employs a tank circuit (parallel LC combination) to
short out signals too high or too low in frequency from
getting to the load:
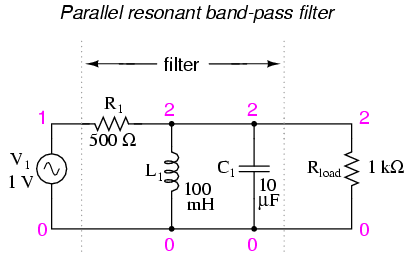
The tank circuit will have a lot of
impedance at resonance, allowing the signal to get to the
load with minimal attenuation. Under or over resonant
frequency, however, the tank circuit will have a low
impedance, shorting out the signal and dropping most of it
across series resistor R1.
parallel resonant bandpass filter
v1 1 0 ac 1 sin
r1 1 2 500
l1 2 0 100m
c1 2 0 10u
rload 2 0 1k
.ac lin 20 50 250
.plot ac v(2)
.end
freq v(2) 3.162E-02 1.000E-01 3.162E-01 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
5.000E+01 6.933E-02 . * . . .
6.053E+01 8.814E-02 . * . . .
7.105E+01 1.100E-01 . .* . .
8.158E+01 1.361E-01 . . * . .
9.211E+01 1.684E-01 . . * . .
1.026E+02 2.096E-01 . . * . .
1.132E+02 2.640E-01 . . * . .
1.237E+02 3.382E-01 . . .* .
1.342E+02 4.392E-01 . . . * .
1.447E+02 5.630E-01 . . . * .
1.553E+02 6.578E-01 . . . * .
1.658E+02 6.432E-01 . . . * .
1.763E+02 5.503E-01 . . . * .
1.868E+02 4.543E-01 . . . * .
1.974E+02 3.792E-01 . . . * .
2.079E+02 3.234E-01 . . * .
2.184E+02 2.816E-01 . . *. .
2.289E+02 2.495E-01 . . * . .
2.395E+02 2.242E-01 . . * . .
2.500E+02 2.038E-01 . . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Load voltage peaks at resonant frequency (159.15 Hz)
Just like the low-pass and high-pass filter
designs relying on a series resistance and a parallel
"shorting" component to attenuate unwanted frequencies, this
resonant circuit can never provide full input (source)
voltage to the load. That series resistance will always be
dropping some amount of voltage so long as there is a load
resistance connected to the output of the filter.
It should be noted that this form of
band-pass filter circuit is very popular in analog radio
tuning circuitry, for selecting a particular radio frequency
from the multitudes of frequencies available from the
antenna. In most analog radio tuner circuits, the rotating
dial for station selection moves a variable capacitor in a
tank circuit.

The variable capacitor and air-core inductor
shown in the above photograph of a simple radio comprise the
main elements in the tank circuit filter used to
discriminate one radio station's signal from another.
Just as we can use series and parallel LC
resonant circuits to pass only those frequencies within a
certain range, we can also use them to block frequencies
within a certain range, creating a band-stop filter. Again,
we have two major strategies to follow in doing this, to use
either series or parallel resonance. First, we'll look at
the series variety:
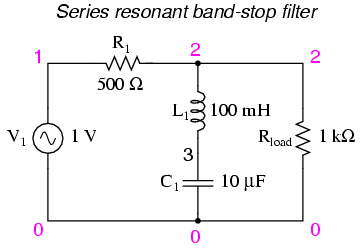
When the series LC combination reaches
resonance, its very low impedance shorts out the signal,
dropping it across resistor R1 and preventing its
passage on to the load.
series resonant bandstop filter
v1 1 0 ac 1 sin
r1 1 2 500
l1 2 3 100m
c1 3 0 10u
rload 2 0 1k
.ac lin 20 70 230
.plot ac v(2)
.end
freq v(2) 1.000E-03 1.000E-02 1.000E-01 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
7.000E+01 3.213E-01 . . . * .
7.842E+01 2.791E-01 . . . * .
8.684E+01 2.401E-01 . . . * .
9.526E+01 2.041E-01 . . . * .
1.037E+02 1.708E-01 . . . * .
1.121E+02 1.399E-01 . . . * .
1.205E+02 1.111E-01 . . .* .
1.289E+02 8.413E-02 . . *. .
1.374E+02 5.887E-02 . . * . .
1.458E+02 3.508E-02 . . * . .
1.542E+02 1.262E-02 . .* . .
1.626E+02 8.644E-03 . *. . .
1.711E+02 2.884E-02 . . * . .
1.795E+02 4.805E-02 . . * . .
1.879E+02 6.638E-02 . . * . .
1.963E+02 8.388E-02 . . *. .
2.047E+02 1.006E-01 . . * .
2.132E+02 1.167E-01 . . .* .
2.216E+02 1.321E-01 . . . * .
2.300E+02 1.469E-01 . . . * .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Notch frequency = LC resonant frequency (159.15 Hz)
Next, we will examine the parallel resonant
band-stop filter:

The parallel LC components present a high
impedance at resonant frequency, thereby blocking the signal
from the load at that frequency. Conversely, it passes
signals to the load at any other frequencies.
parallel resonant bandstop filter
v1 1 0 ac 1 sin
l1 1 2 100m
c1 1 2 10u
rload 2 0 1k
.ac lin 20 100 200
.plot ac v(2)
.end
freq v(2) 3.162E-02 1.000E-01 3.162E-01 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1.000E+02 9.947E-01 . . . * .
1.053E+02 9.932E-01 . . . * .
1.105E+02 9.911E-01 . . . * .
1.158E+02 9.883E-01 . . . * .
1.211E+02 9.841E-01 . . . * .
1.263E+02 9.778E-01 . . . * .
1.316E+02 9.675E-01 . . . * .
1.368E+02 9.497E-01 . . . *. .
1.421E+02 9.152E-01 . . . *. .
1.474E+02 8.388E-01 . . . * . .
1.526E+02 6.420E-01 . . . * . .
1.579E+02 1.570E-01 . . * . . .
1.632E+02 4.450E-01 . . . * . .
1.684E+02 7.496E-01 . . . * . .
1.737E+02 8.682E-01 . . . * . .
1.789E+02 9.201E-01 . . . *. .
1.842E+02 9.465E-01 . . . *. .
1.895E+02 9.616E-01 . . . * .
1.947E+02 9.710E-01 . . . * .
2.000E+02 9.773E-01 . . . * .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Notch frequency = LC resonant frequency (159.15 Hz)
Once again, notice how the absence of a
series resistor makes for minimum attenuation for all the
desired (passed) signals. The amplitude at the notch
frequency, on the other hand, is very low. In other words,
this is a very "selective" filter.
In all these resonant filter designs, the
selectivity depends greatly upon the "purity" of the
inductance and capacitance used. If there is any stray
resistance (especially likely in the inductor), this will
diminish the filter's ability to finely discriminate
frequencies, as well as introduce antiresonant effects that
will skew the peak/notch frequency.
A word of caution to those designing
low-pass and high-pass filters is in order at this point.
After assessing the standard RC and LR low-pass and
high-pass filter designs, it might occur to a student that a
better, more effective design of low-pass or high-pass
filter might be realized by combining capacitive and
inductive elements together like this:
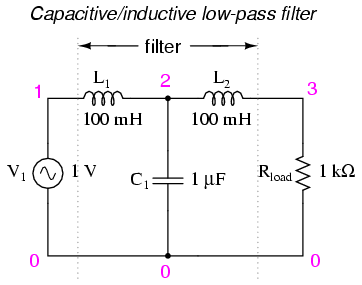
The inductors should block any high
frequencies, while the capacitor should short out any high
frequencies as well, both working together to allow only low
frequency signals to reach the load.
At first, this seems to be a good strategy,
and eliminates the need for a series resistance. However,
the more insightful student will recognize that any
combination of capacitors and inductors together in a
circuit is likely to cause resonant effects to happen at a
certain frequency. Resonance, as we have seen before, can
cause strange things to happen. Let's plot a SPICE analysis
and see what happens over a wide frequency range:
lc lowpass filter
v1 1 0 ac 1 sin
l1 1 2 100m
c1 2 0 1u
l2 2 3 100m
rload 3 0 1k
.ac lin 20 100 1k
.plot ac v(3)
.end
freq v(3) 1.000E-01 3.162E-01 1.000E+00 3.162E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1.000E+02 1.033E+00 . . * .
1.474E+02 1.074E+00 . . .* .
1.947E+02 1.136E+00 . . . * .
2.421E+02 1.228E+00 . . . * .
2.895E+02 1.361E+00 . . . * .
3.368E+02 1.557E+00 . . . * .
3.842E+02 1.853E+00 . . . * .
4.316E+02 2.308E+00 . . . * .
4.789E+02 2.919E+00 . . . *.
5.263E+02 3.185E+00 . . . *
5.737E+02 2.553E+00 . . . * .
6.211E+02 1.802E+00 . . . * .
6.684E+02 1.298E+00 . . . * .
7.158E+02 9.778E-01 . . * .
7.632E+02 7.650E-01 . . * . .
8.105E+02 6.165E-01 . . * . .
8.579E+02 5.084E-01 . . * . .
9.053E+02 4.268E-01 . . * . .
9.526E+02 3.635E-01 . . * . .
1.000E+03 3.133E-01 . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
What was supposed to be a low-pass filter
turns out to be a band-pass filter with a peak somewhere
around 526 Hz! The capacitance and inductance in this filter
circuit are attaining resonance at that point, creating a
large voltage drop around C1, which is seen at
the load, regardless of L2's attenuating
influence. The output voltage to the load at this point
actually exceeds the input (source) voltage! A little more
reflection reveals that if L1 and C2
are at resonance, they will impose a very heavy (very low
impedance) load on the AC source, which might not be good
either. We'll run the same analysis again, only this time
plotting C1's voltage and the source current
along with load voltage:
legend:
*: v(3)
+: v(2)
=: i(v1)
freq v(3)
(*)---------- 1.000E-01 3.162E-01 1.000E+00 3.162E+00
(+)---------- 3.162E-01 1.000E+00 3.162E+00 1.000E+01
(=)---------- 1.000E-03 3.162E-03 1.000E-02 3.162E-02
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1.000E+02 1.033E+00 . = + * .
1.474E+02 1.074E+00 . = .+ .* .
1.947E+02 1.136E+00 . = . + . * .
2.421E+02 1.228E+00 . = . + . * .
2.895E+02 1.361E+00 . = . + . * .
3.368E+02 1.557E+00 . .= + . * .
3.842E+02 1.853E+00 . . = + . * .
4.316E+02 2.308E+00 . . = + . * .
4.789E+02 2.919E+00 . . = + *.
5.263E+02 3.185E+00 . . .x *
5.737E+02 2.553E+00 . . +=. * .
6.211E+02 1.802E+00 . . + = . * .
6.684E+02 1.298E+00 . . + = . * .
7.158E+02 9.778E-01 . .+ = * .
7.632E+02 7.650E-01 . + . = * . .
8.105E+02 6.165E-01 . + = * . .
8.579E+02 5.084E-01 . + =. * . .
9.053E+02 4.268E-01 . + = . * . .
9.526E+02 3.635E-01 . + = . * . .
1.000E+03 3.133E-01 . + = * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Sure enough, we see the voltage across C1
and the source current spiking to a high point at the same
frequency where the load voltage is maximum. If we were
expecting this filter to provide a simple low-pass function,
we might be disappointed by the results.
Despite this unintended resonance, low-pass
filters made up of capacitors and inductors are frequently
used as final stages in AC/DC power supplies to filter the
unwanted AC "ripple" voltage out of the DC converted from
AC. Why is this, if this particular filter design possesses
a potentially troublesome resonant point?
The answer lies in the selection of filter
component sizes and the frequencies encountered from an
AC/DC converter (rectifier). What we're trying to do in an
AC/DC power supply filter is separate DC voltage from a
small amount of relatively high-frequency AC voltage. The
filter inductors and capacitors are generally quite large
(several Henrys for the inductors and thousands of �F for
the capacitors is typical), making the filter's resonant
frequency very, very low. DC of course, has a "frequency" of
zero, so there's no way it can make an LC circuit resonate.
The ripple voltage, on the other hand, is a non-sinusoidal
AC voltage consisting of a fundamental frequency at least
twice the frequency of the converted AC voltage, with
harmonics many times that in addition. For plug-in-the-wall
power supplies running on 60 Hz AC power (60 Hz United
States; 50 Hz in Europe), the lowest frequency the filter
will ever see is 120 Hz (100 Hz in Europe), which is well
above its resonant point. Therefore, the potentially
troublesome resonant point in a such a filter is completely
avoided.
The following SPICE analysis calculates the
voltage output (AC and DC) for such a filter, with series DC
and AC (120 Hz) voltage sources providing a rough
approximation of the mixed-frequency output of an AC/DC
converter.
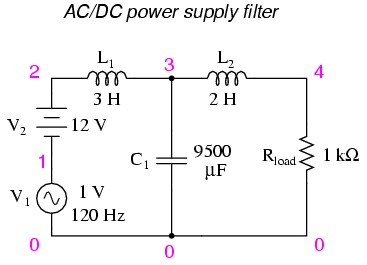
ac/dc power supply filter
v1 1 0 ac 1 sin
v2 2 1 dc
l1 2 3 3
c1 3 0 9500u
l2 3 4 2
rload 4 0 1k
.dc v2 12 12 1
.ac lin 1 120 120
.print dc v(4)
.print ac v(4)
.end
v2 v(4)
1.200E+01 1.200E+01 DC voltage at load = 12 volts
freq v(4)
1.200E+02 3.412E-05 AC voltage at load = 34.12 microvolts
With a full 12 volts DC at the load and only
34.12 �V of AC left from the 1 volt AC source imposed across
the load, this circuit design proves itself to be a very
effective power supply filter.
The lesson learned here about resonant
effects also applies to the design of high-pass filters
using both capacitors and inductors. So long as the desired
and undesired frequencies are well to either side of the
resonant point, the filter will work okay. But if any signal
of significant magnitude close to the resonant frequency is
applied to the input of the filter, strange things will
happen!
|