Why learn about Karnaugh maps? The
Karnaugh map, like Boolean algebra, is a simplification tool applicable to
digital logic. See the "Toxic waste incinerator" in the Boolean algebra
chapter for an example of Boolean simplification of digital logic. The
Karnaugh Map will simplify logic faster and more easily in most cases.
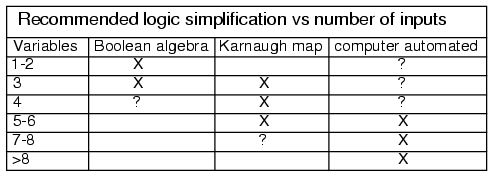
Boolean simplification is actually faster than the Karnaugh map for a
task involving two or fewer Boolean variables. It is still quite usable at
three variables, but a bit slower. At four input variables, Boolean algebra
becomes tedious. Karnaugh maps are both faster and easier. Karnaugh maps
work well for up to six input variables, are usable for up to eight
variables. For more than six to eight variables, simplification should be by
CAD (computer automated design).
In theory any of the three methods will work. However, as a practical
matter, the above guidelines work well. We would not normally resort to
computer automation to simplify a three input logic block. We could sooner
solve the problem with pencil and paper. However, if we had seven of these
problems to solve, say for a BCD (Binary Coded Decimal) to seven
segment decoder, we might want to automate the process. A BCD to seven
segment decoder generates the logic signals to drive a seven segment LED
(light emitting diode) display.
Examples of computer automated design languages for simplification of
logic are PALASM, ABEL, CUPL, Verilog, and VHDL. These programs accept a
hardware descriptor language input file which is based on Boolean
equations and produce an output file describing a reduced (or
simplified) Boolean solution. We will not require such tools in this
chapter. Let's move on to Venn diagrams as an introduction to Karnaugh maps. |