Kirchhoff's Current
Law (KCL)
Let's take a closer look at that last
parallel example circuit:
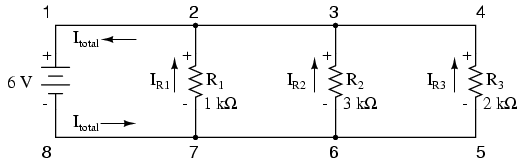
Solving for all values of voltage and
current in this circuit:

At this point, we know the value of each
branch current and of the total current in the circuit. We
know that the total current in a parallel circuit must equal
the sum of the branch currents, but there's more going on in
this circuit than just that. Taking a look at the currents
at each wire junction point (node) in the circuit, we should
be able to see something else:
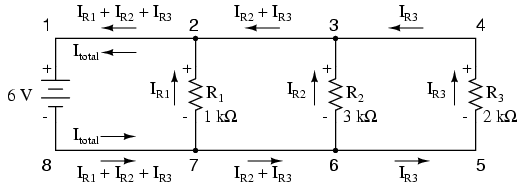
At each node on the negative "rail" (wire
8-7-6-5) we have current splitting off the main flow to each
successive branch resistor. At each node on the positive
"rail" (wire 1-2-3-4) we have current merging together to
form the main flow from each successive branch resistor.
This fact should be fairly obvious if you think of the water
pipe circuit analogy with every branch node acting as a
"tee" fitting, the water flow splitting or merging with the
main piping as it travels from the output of the water pump
toward the return reservoir or sump.
If we were to take a closer look at one
particular "tee" node, such as node 3, we see that the
current entering the node is equal in magnitude to the
current exiting the node:
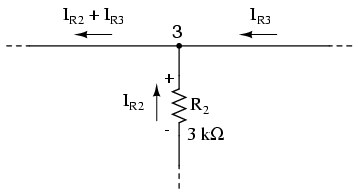
From the right and from the bottom, we have
two currents entering the wire connection labeled as node 3.
To the left, we have a single current exiting the node equal
in magnitude to the sum of the two currents entering. To
refer to the plumbing analogy: so long as there are no leaks
in the piping, what flow enters the fitting must also exit
the fitting. This holds true for any node ("fitting"), no
matter how many flows are entering or exiting.
Mathematically, we can express this general relationship as
such:
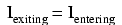
Mr. Kirchhoff decided to express it in a
slightly different form (though mathematically equivalent),
calling it Kirchhoff's Current Law (KCL):
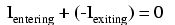
Summarized in a phrase, Kirchhoff's Current
Law reads as such:
"The algebraic sum of all currents
entering and exiting a node must equal zero"
That is, if we assign a mathematical sign
(polarity) to each current, denoting whether they enter (+)
or exit (-) a node, we can add them together to arrive at a
total of zero, guaranteed.
Taking our example node (number 3), we can
determine the magnitude of the current exiting from the left
by setting up a KCL equation with that current as the
unknown value:
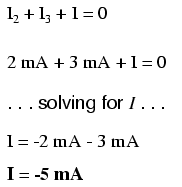
The negative (-) sign on the value of 5
milliamps tells us that the current is exiting the
node, as opposed to the 2 milliamp and 3 milliamp currents,
which must were both positive (and therefore entering
the node). Whether negative or positive denotes current
entering or exiting is entirely arbitrary, so long as they
are opposite signs for opposite directions and we stay
consistent in our notation, KCL will work.
Together, Kirchhoff's Voltage and Current
Laws are a formidable pair of tools useful in analyzing
electric circuits. Their usefulness will become all the more
apparent in a later chapter ("Network Analysis"), but
suffice it to say that these Laws deserve to be memorized by
the electronics student every bit as much as Ohm's Law.
|