Capacitor transient response
Because capacitors store energy in the form
of an electric field, they tend to act like small
secondary-cell batteries, being able to store and release
electrical energy. A fully discharged capacitor maintains
zero volts across its terminals, and a charged capacitor
maintains a steady quantity of voltage across its terminals,
just like a battery. When capacitors are placed in a circuit
with other sources of voltage, they will absorb energy from
those sources, just as a secondary-cell battery will become
charged as a result of being connected to a generator. A
fully discharged capacitor, having a terminal voltage of
zero, will initially act as a short-circuit when attached to
a source of voltage, drawing maximum current as it begins to
build a charge. Over time, the capacitor's terminal voltage
rises to meet the applied voltage from the source, and the
current through the capacitor decreases correspondingly.
Once the capacitor has reached the full voltage of the
source, it will stop drawing current from it, and behave
essentially as an open-circuit.

When the switch is first closed, the voltage
across the capacitor (which we were told was fully
discharged) is zero volts; thus, it first behaves as though
it were a short-circuit. Over time, the capacitor voltage
will rise to equal battery voltage, ending in a condition
where the capacitor behaves as an open-circuit. Current
through the circuit is determined by the difference in
voltage between the battery and the capacitor, divided by
the resistance of 10 kΩ. As the capacitor voltage approaches
the battery voltage, the current approaches zero. Once the
capacitor voltage has reached 15 volts, the current will be
exactly zero. Let's see how this works using real values:
---------------------------------------------
| Time | Battery | Capacitor | Current |
|(seconds) | voltage | voltage | |
|-------------------------------------------|
| 0 | 15 V | 0 V | 1500 uA |
|-------------------------------------------|
| 0.5 | 15 V | 5.902 V | 909.8 uA |
|-------------------------------------------|
| 1 | 15 V | 9.482 V | 551.8 uA |
|-------------------------------------------|
| 2 | 15 V | 12.970 V | 203.0 uA |
|-------------------------------------------|
| 3 | 15 V | 14.253 V | 74.68 uA |
|-------------------------------------------|
| 4 | 15 V | 14.725 V | 27.47 uA |
|-------------------------------------------|
| 5 | 15 V | 14.899 V | 10.11 uA |
|-------------------------------------------|
| 6 | 15 V | 14.963 V | 3.718 uA |
|-------------------------------------------|
| 10 | 15 V | 14.999 V | 0.068 uA |
---------------------------------------------
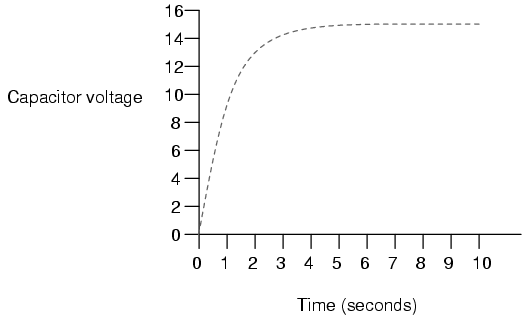
The capacitor voltage's approach to 15 volts
and the current's approach to zero over time is what a
mathematician would call asymptotic: that is, they
both approach their final values, getting closer and closer
over time, but never exactly reaches their destinations. For
all practical purposes, though, we can say that the
capacitor voltage will eventually reach 15 volts and that
the current will eventually equal zero.
Using the SPICE circuit analysis program, we
can chart this asymptotic buildup of capacitor voltage and
decay of capacitor current in a more graphical form
(capacitor current is plotted in terms of voltage drop
across the resistor, using the resistor as a shunt to
measure current):
capacitor charging
v1 1 0 dc 15
r1 1 2 10k
c1 2 0 100u ic=0
.tran .5 10 uic
.plot tran v(2,0) v(1,2)
.end
legend:
*: v(2) Capacitor voltage
+: v(1,2) Capacitor current
time v(2)
(*+)----------- 0.000E+00 5.000E+00 1.000E+01 1.500E+01
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 5.976E-05 * . . +
5.000E-01 5.881E+00 . . * + . .
1.000E+00 9.474E+00 . .+ *. .
1.500E+00 1.166E+01 . + . . * .
2.000E+00 1.297E+01 . + . . * .
2.500E+00 1.377E+01 . + . . * .
3.000E+00 1.426E+01 . + . . * .
3.500E+00 1.455E+01 .+ . . *.
4.000E+00 1.473E+01 .+ . . *.
4.500E+00 1.484E+01 + . . *
5.000E+00 1.490E+01 + . . *
5.500E+00 1.494E+01 + . . *
6.000E+00 1.496E+01 + . . *
6.500E+00 1.498E+01 + . . *
7.000E+00 1.499E+01 + . . *
7.500E+00 1.499E+01 + . . *
8.000E+00 1.500E+01 + . . *
8.500E+00 1.500E+01 + . . *
9.000E+00 1.500E+01 + . . *
9.500E+00 1.500E+01 + . . *
1.000E+01 1.500E+01 + . . *
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
As you can see, I have used the .plot
command in the netlist instead of the more familiar
.print command. This generates a pseudo-graphic plot of
figures on the computer screen using text characters. SPICE
plots graphs in such a way that time is on the vertical axis
(going down) and amplitude (voltage/current) is plotted on
the horizontal (right=more; left=less). Notice how the
voltage increases (to the right of the plot) very quickly at
first, then tapering off as time goes on. Current also
changes very quickly at first then levels off as time goes
on, but it is approaching minimum (left of scale) while
voltage approaches maximum.
-
REVIEW:
-
Capacitors act somewhat like
secondary-cell batteries when faced with a sudden change
in applied voltage: they initially react by producing a
high current which tapers off over time.
-
A fully discharged capacitor initially
acts as a short circuit (current with no voltage drop)
when faced with the sudden application of voltage. After
charging fully to that level of voltage, it acts as an
open circuit (voltage drop with no current).
-
In a resistor-capacitor charging circuit,
capacitor voltage goes from nothing to full source voltage
while current goes from maximum to zero, both variables
changing most rapidly at first, approaching their final
values slower and slower as time goes on.
|