A memory is neither a sequential circuit (since we require sequential circuits to be clocked, and memories are not clocked), nor a combinatorial circuit, since its output values depend on past values.

In general, a memory has m inputs that are called the address inputs that are used to select exactly one out of 2^m words, each one consisting of n bits.

Furthermore, it has n connectors that are bidirectional that are called the data lines. These data lines are used both as inputs in order to store information in a word selected by the address inputs, and as outputs in order to recall a previously stored value. Such a solution reduces the number of required connectors by a factor two.

Finally, it has an input called enable (see the section on tri-state logic for an explanation) that controls whether the data lines have defined states or not, and an input called r/w that determines the direction of the data lines.

A memory with an arbitrary value of m and an arbitrary value of n can be built from memories with smaller values of these parameters. To show how this can be done, we first show how a one-bit memory (one with m = 0 and n = 1) can be built. Here is the circuit:

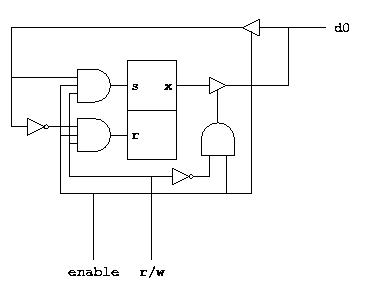
The central part of the circuit is an SR-latch that holds one bit of information. When enable is 0, the output d₀ is isolated both from the inputs to and the output from the SR-latch. Information is passed from d₀ to the inputs of the latch when enable is 1 and r/w is 1 (indicating write). Information is passed from the output x to d₀ when enable is 1 and r/w is 0 (indicating read).

Now that we know how to make a one-bit memory, we must figure out how to make larger memories. First, suppose we have n memories of 2^m words, each one consisting of a single bit. We can easily convert these to a single memory with 2^m words, each one consisting of a n bits. Here is how we do it:

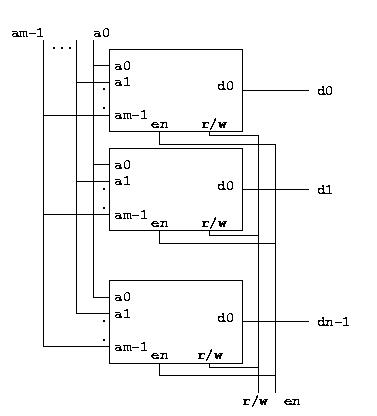
We have simply connected all the address inputs together, all the enables together, and all the read/writes together. Each one-but memory supplies one of the bits of the n-bit word in the final circuit.

Next, we have to figure out how to make a memory with more words. To show that, we assume that we have two memories each with m address inputs and n data lines. We show how we can connect them so as to obtain a single memory with m + 1 address inputs and n data lines. Here is the circuit:

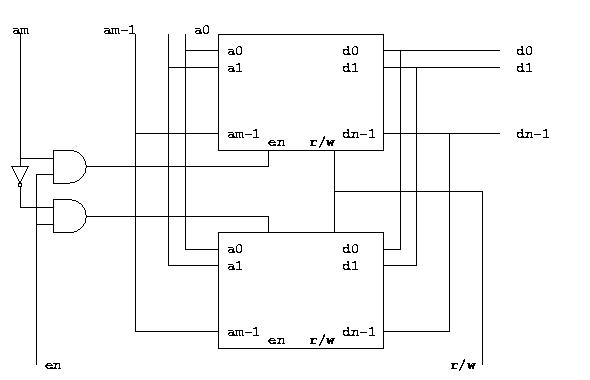
As you can see, the additional address line is combined with the enable input to select one of the two smaller memories. Only one of them will be connected to the data lines at a time (because of the way tri-state logic works).