Gates - Digital Circuits

The basic building blocks of a computer are called logical gates or just gates.

Gates are basic circuits that have at least one (and usually more) input and exactly one output. Input and output values are the logical values true and false. In computer architecture it is common to use 0 for false and 1 for true. Gates have no memory. The value of the output depends only on the current value of the inputs. This fact makes it possible to use a truth table to fully describe the behavior of a gate.

We usually consider three basic kinds of gates, and-gates, or-gates, and not-gates (or inverters).

Basic gates

An and-gate has an arbitrary number of inputs. The output value is 1 if and only if all of the inputs are 1. Otherwise the output value is 0. The name has been chosen because the output is 1 if and only if the first input and the second input, and, ..., and the nth input are all 1.

It is often useful to draw diagrams of gates and their interconnections. In such diagrams, the and-gate is drawn like this:

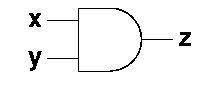
The truth table for an and-gate with two inputs looks like this:

   x y | z
   -------
   0 0 | 0
   0 1 | 0
   1 0 | 0
   1 1 | 1

Like the and-gate, the or-gate can have an arbitrary number of inputs. The output value is 1 if and only of at least one of the input values are 1. Otherwise the output is 0. In other words, the output value is 0 only if all inputs are 0. The name has been chosen because the output is 1 if and only if the first input or the second input, or, ..., or the nth input is 1.

In circuit diagrams, we draw the or-gate like this:

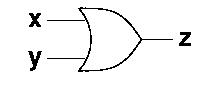
The truth table for an or-gate with two inputs looks like this:

   x y | z
   -------
   0 0 | 0
   0 1 | 1
   1 0 | 1
   1 1 | 1

An inverter has exactly one input and one output. The value of the output is 1 if and only if the input is 0. Otherwise, the output is 0. In other words, the value of the output is the exact opposite of the value of the input.

In circuit diagrams, we draw the inverter like this:

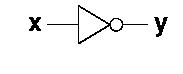
The truth table for an inverter looks like this:

   x | y
   -----
   0 | 1
   1 | 0

Sometimes, it is practical to combine functions of the basic gates into more complex gates, for instance in order to save space in circuit diagrams. In this section, we show some such combined gates together with their truth tables.

The nand-gate is an and-gate with an inverter on the output. So instead of drawing several gates like this:

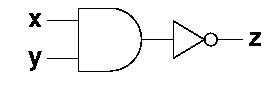
We draw a single and-gate with a little ring on the output like this:

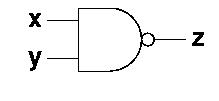
The nand-gate, like the and-gate can take an arbitrary number of inputs.

The truth table for the nand-gate is like the one for the and-gate, except that all output values have been inverted:

   x y | z
   -------
   0 0 | 1
   0 1 | 1
   1 0 | 1
   1 1 | 0

The nor-gate is an or-gate with an inverter on the output. So instead of drawing several gates like this:

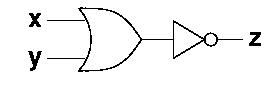
We draw a single or-gate with a little ring on the output like this:

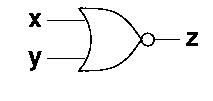
The nor-gate, like the or-gate can take an arbitrary number of inputs.

The truth table for the nor-gate is like the one for the or-gate, except that all output values have been inverted:

   x y | z
   -------
   0 0 | 1
   0 1 | 0
   1 0 | 0
   1 1 | 0

The exclusive-or-gate is similar to an or-gate. It can have an arbitrary number of inputs, and its output value is 1 if and only if exactly one input is 1 (and thus the others 0). Otherwise, the output is 0.

We draw an exclusive-or-gate like this:

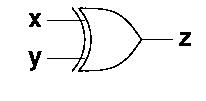
The truth table for an exclusive-or-gate with two inputs looks like this:

   x y | z
   -------
   0 0 | 0
   0 1 | 1
   1 0 | 1
   1 1 | 0

A valid question at this point is how many different kinds of gates there are, and what they are called.

Let us limit ourselves to gates with n inputs. The truth tables for such gates have 2ⁿ lines. Such a gate is completely defined by the output column in the truth table. The output column can be viewed as a string of 2ⁿ binary digits. How many different strings of binary digits of length 2ⁿ are there? The answer is 2^2ⁿ, since there are 2^k different strings of k binary digits, and if k=2ⁿ, then there are 2^2ⁿ such strings. In particular, if n=2, we can see that there are 16 different types of gates with 2 inputs.

Most of these gates do not have any names, and indeed, most of them are quite useless. For completeness, let us look at all 16 and study the functions they compute. Each entry in the following table is specified by the output string:

0000 A gate that ignores both its inputs and always gives 0 on the output. This gate does not require any circuits. Just let the inputs hang and connect the output to a 0.
0001 This is the and-gate described above.
0010 This is like an and-gate with an inverter on the second input.
0011 This gate ignores its second input, and gives as output the value of its first input. It does not require any circuits. Just connect the output to the first input and let the second input hang.
0100 This is like an and-gate with an inverter on the first input.
0101 This gate ignores its first input, and gives as output the value of its second input. It does not require any circuits. Just connect the output to the second input and let the first input hang.
0110 This is the exclusive-or-gate described above.
0111 This is the or-gate described above.
1000 This is the nor-gate described above.
1001 This is like an exclusive-or-gate with an inverter on its output.
1010 This gate can be built with an inverter on the second input, and with the first input hanging.
1011 This is like an or-gate with an inverter on its second input.
1100 This gate can be built with an inverter on the first input, and with the second input hanging.
1101 This is like an or-gate with an inverter on its first input.
1110 This is the nand-gate described above.
1111 This is a gate that ignores both its inputs and always gives a 1 as output. This gate does not require any circuits. Just let the inputs hang and connect the output to a 1.

As you can see, most of the gates possible, are quite useless.

As it turns out, it is possible to build any kind of gate using only nand-gates. To see this, first observe that an inverter is just a nand-gate with only one input. Second, an and-gate can be built as a nand with an inverter on its output. Last, an or-gate can be build with a nand-gate with an inverter on each input.

In some circuit technology, it is actually easier to build a nand-gate than any of the other gates. In that case, the nand-gate is considered the most primitive building block, and everything else is built from it.

Similarly, all gates can be realized from only nor-gates. Again an inverter is just a nor-gate with only one input. An or-gate is a nor-gate with an inverter on its output, and an and-gate is just a nor-gate with an inverter on each input.

Although gates can be arbitrarily complicated, from now on when we say gates we mean one of inverter, and, or, nand, nor, and sometimes exclusive or.

So why do we want to exclude other gates? The main reason is that we want the number of gates of a circuit to reflect the cost of fabrication of that circuit. If we allow arbitrarily complicated gates, we can design an arbitrarily complicated combinatorial circuit with only one gate.

Our restriction above is not ideal, since in order for the number of gates to reflect the cost, we would have to take the particular technology used for fabrication into account. Different circuits are easy to make in different technologies. But in order to remain somewhat independent of specific technology, we use this approximation.